The existence that generates language
2018-2019
-----------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------
References
Reference is cited from the papers written
at SekinanLibrary and SRFL
28 February 2019
---------------------------------------------------------------------------------------------------------------------------
Main Issue 1
Quantum Group Language
Main Issue is written titled as Quantum group language
abbreviated to QGL.
2 March 2019
---------------------------------------------------------------------------------------------------------------------------
Main Issue 2
The Premise for Quantum Group Language
Contents
Derived Category Language, 23 July 2016 Edition
Read more: https://srfl-theory.webnode.com/news/derived-category-language-23-july-2016-edition/
Text
1
Bridge across mathematics and physics / Revised
3
Derived Category Language 1 |
Category theoretic mirror symmetry conjecture
1.
Fukaya category is
Fuk(X, ω).
Fukaya category is
Fuk(X, ω).
2.
General symplectic manifold is .
.
3.
General symplectic manifold is
 .
.3.
Derived category of A∞ is
is  .
.
 is
is  .
.
4.
Conjecture
Conjecture
When
 and
and 
have physical mirror relation,
there exists the next triangle category's equivalence

[Reference 1]
[References 2]
- Bridge across mathematics and physics
- Kontsevich's conjecture Category theoretic mirror symmetry conjecture
Tokyo
18 May 2016
4
Karcevskij conjecture 1928 and Kawamata conjecture 2002
TANAKA Akio
Sergej Karcevskij declared a conjecture for language's asymmetric structure on the TCLP of the Linguistic Circle of Prague in 1928. I briefly wrote about the conjecture as the following.
.....................................................................................................................................
Prague in 1920s, The Linguistic Circle of Prague and Sergej Karcevskij's paper "Du dualisme asymetrique du signe linguistique"
From Print 2012, Chapter 18
Non-symmetry. It was the very theme that I repeatedly talked on with C. Prague in 1920s. Karcevskij's paper "Du dualisme asymetrique du signe linguistique" that appeared in the magazine TCLP. Absolutely contradicted coexistence between flexibility and solidity, which language keeps on maintaining, by which language continues existing as language. Still now there will exist the everlasting dual contradiction in language. Why can language stay in such solid and such flexible condition like that. Karcevskij proposed the duality that is seemed to be almost absolute contradiction. Sergej Karcevskij's best of papers, for whom C called as the only genius in his last years' book Janua Linguisticae reserata 1994.
Source:
Reference:
Reference 2:
References 3:
References 4:
Reference 5:
[Note, 2 October 2014]
In this Tale, Print 2012, C is CHINO Eiichi who was the very teacher in my life, taught me almost all the heritage of modern linguistics. I first met him in 1969 at university's his Russian class as a student knowing nothing on language study.
Tokyo
23 February 2015
SIL
....................................................................................................................................
This asymmetric duality of linguistic sign presented by Karcevskij has become the prime mover for my study from the latter half of the 20th century being led by my teacher CHINO Eiichi.
But the theme was very hard even to find a clue. The turning point visited after I again learnt mathematics especially algebraic geometry in 1980s.
In 2009 I successively wrote the trial papers of the theme assisted by several results of contemporary mathematics. The papers are the following.
......................................................................................................................................
The papers on this site have been published by
Sekinan Research Field of Language
Sekinan Research Field of Language
....................................................................................................................................
Entering in this year 2016, I read TODA Yukinobu's book, Several Problems on Derived Category of Coherent sheaf, Tokyo, 2016. The book shows me the update overview on derived category of coherent sheaf. The essence of my notable points are noted at the following.
....................................................................................................................................
............................................................................................................................................
In the TODA's book, I received the great hint on Karcevskij's conjecture for language's hard problem.
The hint exists at Kawamata conjecture presented in 2002. The details are the following.
............................................................................................................................................
Derived Category Language 2

 .
.
 .
.
Kontsevich's conjecture
Category theoretic mirror symmetry conjecture
When there exists mirror relation between X1 and X2, derived category of X1's coherent sheaf and derived Fukaya category defined from X2's symplectic structure become equivalence.
M. Kontsevich. Homological algebra of mirror symmetry, Vol. 1 of Proceedings of ICM. 1995.
-----------------------------------------------------------------------------------------------------------------------
[Note by TANAKA Akio]
In the near future, symplectic geometry may be written by derived category. If so, complexed image of symplectic geometry's some theorems will become clearer.
References
Mirror Symmetry Conjecture on Rational Curve / Symplectic Language Theory / 27 February 2009
Category theoretic mirror symmetry conjecture
When there exists mirror relation between X1 and X2, derived category of X1's coherent sheaf and derived Fukaya category defined from X2's symplectic structure become equivalence.
M. Kontsevich. Homological algebra of mirror symmetry, Vol. 1 of Proceedings of ICM. 1995.
-----------------------------------------------------------------------------------------------------------------------
[Note by TANAKA Akio]
In the near future, symplectic geometry may be written by derived category. If so, complexed image of symplectic geometry's some theorems will become clearer.
References
Mirror Symmetry Conjecture on Rational Curve / Symplectic Language Theory / 27 February 2009
............................................................................................................................................
In the TODA's book, I received the great hint on Karcevskij's conjecture for language's hard problem.
The hint exists at Kawamata conjecture presented in 2002. The details are the following.
............................................................................................................................................
Derived Category Language 2
Kawamata Conjecture
Conjecture

is birational map between smooth objective algebraic manifolds.
And
 .
.
At This condition,
there exists next fully faithful embedding.
 .
.
[Reference]
- TODA Yukinobu. Several problems on derived category of coherent sheaf. Tokyo, 2016.Chapter 6, Derived category of coherent sheaf and birational geometry, page 148, Conjecture 6.43.
- Bridge across mathematics and physics
- Kontsevich's conjecture Category theoretic mirror symmetry conjecture
Tokyo
19 May 2016
............................................................................................................................
Kawamata conjecture will hint me the new meaning's entrance in the old meaning at a word.
Notes for KARCEVSKIJ Sergej that I ever wrote will be newly revised through TODA's fine work over viewing the recent 20 year development on derived category that began by Grothendieck.
For TODA's book, refer to the next my short essay.
...........................................................................................................................................
For TODA's book, refer to the next my short essay.
...........................................................................................................................................
Bridge across mathematics and physics / Revised
Read more: https://srfl-theory.webnode.com/news/karcevskij-conjecture-1928-and-kawamata-conjecture-2002/
5
Additional meaning and embedding
1.Derived category
Category theoretic mirror symmetry conjecture
1.
Fukaya category is
Fuk(X, ω).
Fuk(X, ω).
2.
General symplectic manifold is .
.
3.
General symplectic manifold is
 .
.3.
Derived category of A∞ is
is  .
.
 is
is  .
.
4.
Conjecture
Conjecture
When
 and
and 
have physical mirror relation,
there exists the next triangle category's equivalence

2.Embedding
Derived Category Language 2
Kawamata Conjecture
Conjecture

is birational map between smooth objective algebraic manifolds.
And
 .
.
At This condition,
there exists next fully faithful embedding.

3.Stable and mobile
[Preparation]
Graded differential algebra 

Minimal model of graded differential algebra 

Degree of homogenious element x of graded differential algabra |x|
Basis of linear space is given by homogenious and elements x1, ....., xn
Λ (V) = Λ(V)k =Λ (x1, ....., xn )
Operation of minimal model 

<Example>
Spherical surface Sn, n≥2
de Rham complex  *(Sn)
*(Sn)
 *(Sn)
*(Sn)
When n is even number,
Volume element of Sn 

Mn = Λ (x), |x| = n, dx = 0,



 ,
, 

M2n-1 gives minimal model Sn to de Rham complex  .
.
 .
.
When n is odd number,
Mn gives minimal model Sn to de Rham complex  .
.
 .
.
[Interpretation]
Word is given by spherical surface.
Meaning of word is given by elements x1, ....., xn.
Word has minimal model.
Word becomes formal.
Fundamental group of word contains free group of rank b1(M).
Here KARCEVSKIJ's "stable part" is identified to fundamental group and " mobile part" is identified to free group.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
All rights reserved.
© 2011 by The Sekinan Research Field of Language
4.Additional meaning
For the Supposition of KARCEVSKIJ Sergej
Completion of Language
September 23, 2011
[Preparation]
1.
n dimensional complex space Cn
Open set 

Whole holomorphic function over U 

Ring sheaf for 

U →Oan(U)
Complex analytic manifold Cann
Algebraic manifold An multinomial of Cann
Ideal of multinomial ring a  [x1, x2, ..., xn]
[x1, x2, ..., xn]
 [x1, x2, ..., xn]
[x1, x2, ..., xn]
V(a) = {(a1, a2, ..., an)  Cn f (a1, a2, ..., an) = 0,
Cn f (a1, a2, ..., an) = 0,  a }
a }
 Cn f (a1, a2, ..., an) = 0,
Cn f (a1, a2, ..., an) = 0,  a }
a }
Whole closed set of V(a) 

Fundamental open set D(f) = {(a1, a2, ..., an)  Cn | f (a1, a2, ..., an) ≠ 0}
Cn | f (a1, a2, ..., an) ≠ 0}
 Cn | f (a1, a2, ..., an) ≠ 0}
Cn | f (a1, a2, ..., an) ≠ 0}
Arbitrary family of open set {Ui} 

Easy sheaf F 

Zariski topological space 

Ring sheaf O
Affine space An = (  , O)
, O)
 , O)
, O)
Ring R
Set of whole maximum ideal Spm R1
Spm R Spectrum of R
<Proposition>
Spm R is Noether- like.
◊
<Proposition>
R is integral domain.
Whole of open sets without null set Ux
Quotient field K
Mapping from Ux to whole partial set of K O
O(V(a)c) =  Rf
Rf
 Rf
Rf
c expresses complementary set.
O is easy sheaf of ring over Spm R that is whole set K.
◊
<Definition>
R is finite generative integral domain over k.
Triple (i) (ii) (iii) is called affine algebraic variety.
(i) Set Spm R
(ii) Zariski topology
(iii) Ring's sheaf O
O is called structure sheaf of affine algebraic variety.
◊
Ring homomorphism between definite generative integral domains 


Upper is expressed by  .
.
 .
.
Ring holomorphism OX(U) → OY((t )-1U)
)-1U)
 )-1U)
)-1U)
Morphism from affine algebraic variety Y to X ( OX(U) → OY((t )-1U), X→Y )
)-1U), X→Y )
 )-1U), X→Y )
)-1U), X→Y )
When  is surjection, t
is surjection, t is isomorphism overclosed partial set defined by p= Ker
is isomorphism overclosed partial set defined by p= Ker  .
.
 is surjection, t
is surjection, t is isomorphism overclosed partial set defined by p= Ker
is isomorphism overclosed partial set defined by p= Ker  .
.
Upper is called to closed immersion.
2.
Ring holomorphism 

Morphism between affine algebraic varieties 

Kernel of  p
p
 p
p
Image of 



<Definition>
It is called that when  is injection
is injection  is dominant.
is dominant.
 is injection
is injection  is dominant.
is dominant.
◊
<Definition>
R is medium ring between S and its quotient field K.
When  that is given by natural injection
that is given by natural injection  is isomorphism over open set,
is isomorphism over open set,  is called open immersion.
is called open immersion.
 that is given by natural injection
that is given by natural injection  is isomorphism over open set,
is isomorphism over open set,  is called open immersion.
is called open immersion.
◊
<Definition>
When X is algebraic variety, longitude of maximum chain is equal to transcendental dimension of function field k(X).
It is called dimension of algebraic variety X, expressed by dim X.
◊
<Definition>
Defined generative field over k K
Space ( X, Ox )added ring that is whole sets of K that has open covers {Ui} satisfies next conditions is called algebraic variety.
satisfies next conditions is called algebraic variety.
 satisfies next conditions is called algebraic variety.
satisfies next conditions is called algebraic variety.
(i) Each Ui is affine algebraic variety that has quotient K .
(ii) For each i, j  I, intersection
I, intersection  is open partial set of
is open partial set of  .
.
 I, intersection
I, intersection  is open partial set of
is open partial set of  .
.
◊
3.
<Definition>
Tensor product between ring and itself becomes ring by each elements products.
Elements  that defines surjective homomorphism is expressed by
that defines surjective homomorphism is expressed by  .
.
 that defines surjective homomorphism is expressed by
that defines surjective homomorphism is expressed by  .
.
Image  of closed embedding defined by
of closed embedding defined by  is called diagonal.
is called diagonal.
 of closed embedding defined by
of closed embedding defined by  is called diagonal.
is called diagonal.
◊
<Definition>
Field K
Ringed space that have common whole set K (A, OA) (B, OB)
Topological space C
Open embedding 

A and B have common partial set C.
Topological space glued A and B by C 

Easy sheaf over W OW
ahere, arbitrary open set Ø ≠ 


Ringed space  is called glue of A and B by C.
is called glue of A and B by C.
 is called glue of A and B by C.
is called glue of A and B by C.
◊
<Definition>
Intedgral domains that have common quotient field K R, S
Element R am ≠ 0
Element S bn ≠ 0

Spm T  Spm R, Spm T
Spm R, Spm T  Spm S
Spm S
 Spm R, Spm T
Spm R, Spm T  Spm S
Spm S
Glue defined by the upper is called simple.
◊
<Definition>
Affine algebraic varieties U1, U2
Common open set of U1, U2 UC
Diagonal embedding 

When the upper is closed set, glue is called separated.
◊
<Proposition>
For simple glue  , next is equivalent.
, next is equivalent.
 , next is equivalent.
, next is equivalent.
(*) It is separated.
(**) Ring  is generated by R and S.
is generated by R and S.
 is generated by R and S.
is generated by R and S.
◊
<Definition>
R and S are integral domains that have common quotient field K.
For partial ring T=RS generated by R and S, when <Definition> simple is satisfied, it is called "Spm R ad Spm S are simple glue."
◊
<Sample>
Projective space Pn is simple glue.
◊
<Definition>
Algebraic Variety's morphism is glue of affine algebraic variety's ring homomorphism image.
Algebraic direct product is direct product of affine algebraic variety.
◊
4.
Affine algebraic variety X
Ring over k R
 is called R value point of X.
is called R value point of X.
Whole  is called set of R value point of X, expressed by X(R).
is called set of R value point of X, expressed by X(R).
 is called set of R value point of X, expressed by X(R).
is called set of R value point of X, expressed by X(R).
Ring homomorphism over k 

X(f) := X(R) X(S)
X(S)
 X(S)
X(S)
Ring homomorphism  ,
, 
 ,
, 

<Definition>
 is function from ring category over k to category of set.
is function from ring category over k to category of set.
◊
<Definition>
Functors from ring category to set category F, G
Ring R
Family of  over ring R {
over ring R { }
}
 over ring R {
over ring R { }
}
{ }
} has functional morphism.
has functional morphism.
 }
} has functional morphism.
has functional morphism.
Functors F,G have isomorphism ( or natural transformation).
Functor from ring's category to set's category that is isomorphic to algebraic variety, is called representable or represent by X, or fine moduli.
◊
<Definition>
Functor from ring's category to set's category F
When  satisfies the next conditions, X is called coarse moduli.
satisfies the next conditions, X is called coarse moduli.
 satisfies the next conditions, X is called coarse moduli.
satisfies the next conditions, X is called coarse moduli.
(i) There is natural transformation  :
:  .
.
 :
:  .
.
(ii) Natural transformation  ,
,
 ,
,
Morphism that satisfies  is existent uniquely.
is existent uniquely.
 is existent uniquely.
is existent uniquely.
(iii) For algebraic close field k'  k,
k,  (k') is always bijection.
(k') is always bijection.
 k,
k,  (k') is always bijection.
(k') is always bijection.
◊
<Definition>
Algebraic variety G that  is functor to group's category is called algebraic group.
is functor to group's category is called algebraic group.
 is functor to group's category is called algebraic group.
is functor to group's category is called algebraic group.
◊
<Definition>
Finite generative ring over k A
When G = Spm A satisfies 3 conditions on the next triad is called affine algebraic group.
Triad



Conditions
(i)  are commutative for
are commutative for  .
.
 are commutative for
are commutative for  .
.
(ii)There is identity map for A.
(iii) There is coincident with  for A.
for A.
 for A.
for A.
◊
5.
Projective space over C Pn
(2n+1) dimensional spherical surface  {
{ }
}
 {
{ }
}
Pn has continuous surjection from  .
.
 .
.
Pn is compact.
<Definition>
Map  is called closed map when
is called closed map when  is closed set image
is closed set image  becomes closed set.
becomes closed set.
 is called closed map when
is called closed map when  is closed set image
is closed set image  becomes closed set.
becomes closed set.
◊
<Definition>
Algebraic variety X is called complete when projection  is closed map for arbitrary manifold Y.
is closed map for arbitrary manifold Y.
 is closed map for arbitrary manifold Y.
is closed map for arbitrary manifold Y.
◊
<Definition>
Morphism from complete algebraic manifold X to separated algebraic manifold Y,  is closed map.
is closed map.
 is closed map.
is closed map.
◊
<Proposition>
Projective space Pn is complete.
◊
<System>
Algebraic manifold that has closed embedding at Pn is complete.
This algebraic manifold is called projective algebraic manifold.
[Interpretation]
Here language is expressed by Pn.
Word is expressed by projective algebraic manifold.
Meaning of word is expressed by closed embedding.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
All rights reserved.
© 2011 by The Sekinan Research Field of Language
5.
Note
Provisional philosophic conjecture on additional meaning is the following.
- From symplectic geometry to Fukaya category.
- From Fukaya category to derived category.
- Kawamata conjecture at derived category.
- Smooth objective algebraic manifolds satisfies birational map.
- Fully faithful embedding exists between two manifolds.
Birational Language
Notes for KARCEVSKIJ Sergej
Stable and Unstable of Language
Symplectic Language Theory
Floer Homology Language
Notes for KARCEVSKIJ Sergej
Stable and Unstable of Language
Symplectic Language Theory
Floer Homology Language
Tokyo
23 May 2016
6
Derived Category Language 2
Kawamata Conjecture
Conjecture

is birational map between smooth objective algebraic manifolds.
And
 .
.
At This condition,
there exists next fully faithful embedding.
 .
.
[Reference]
- TODA Yukinobu. Several problems on derived category of coherent sheaf. Tokyo, 2016.Chapter 6, derived category of coherent sheaf and birational geometry page 148 Conjecture 6.43.
[References 2]
- Bridge across mathematics and physics
- Kontsevich's conjecture Category theoretic mirror symmetry conjecture
Tokyo
19 May 2016
Read more: https://srfl-theory.webnode.com/news/derived-category-language-2-kawamata-conjecture/
7
Language stability and triangulated category
T. Bridgeland defined stability conditions on triangulated categories in 2007.
Language's stability presented by Sergej Karcevskij in 1928.
Bridgeland's stability seems to hint for Karcevskij's stability.
This paper is unfinished.
Tokyo
23 May 2016
SRFL Theory
Language's stability presented by Sergej Karcevskij in 1928.
Bridgeland's stability seems to hint for Karcevskij's stability.
This paper is unfinished.
Tokyo
23 May 2016
SRFL Theory
Read more: https://srfl-theory.webnode.com/news/language-stability-and-triangulated-category/
8
 is bounded kernel of t-structure.
is bounded kernel of t-structure. gives stability condition on A .
gives stability condition on A .
2.
[Paper on Karcevskij conjecture by TANAKA Akio 2011]



 ,
, 

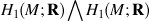 is identified as the partial space of £(
is identified as the partial space of £( 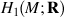 ) that quadrastic Lie bracket of
) that quadrastic Lie bracket of 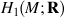 generates.
generates.
Read more: https://srfl-theory.webnode.com/news/derived-category-language-3/
Language stability and triangulated category
[Epitome]
T. Bridgeland defined stability conditions on triangulated categories in 2007.
Language's stability presented by Sergej Karcevskij in 1928.
Bridgeland's stability seems to hint for Karcevskij's stability.
Language's stability presented by Sergej Karcevskij in 1928.
Bridgeland's stability seems to hint for Karcevskij's stability.
Stability conditions on triangulated categories Data ( Z, A ) satisfies the next condition.
 is bounded kernel of t-structure.
is bounded kernel of t-structure. gives stability condition on A .
gives stability condition on A .
------------------------------------------------------------------------------------------------------
2.
[Paper on Karcevskij conjecture by TANAKA Akio 2011]
Condition of Meaning
TANAKA Akio
September 11, 2011
TANAKA Akio
September 11, 2011
[Preparation]
Graded differential algebra 

Minimal model of graded differential algebra 

Degree of homogenious element x of graded differential algabra |x|
Basis of linear space is given by homogenious and elements x1, ....., xn
N (V) = L (V) k = N ( x 1 , ....., x n )
Operation of minimal model 

Spherical surface Sn, n≥2
de Rham complex  *(Sn)
*(Sn)
 *(Sn)
*(Sn)
When n iseaven number,
Volume element of Sn 

Mn = Λ (x), |x| = n, dx = 0,



 ,
, 

M2n-1 gives minimal model Sn to de Rham complex  .
.
 .
.
When n is odd number,
Mn gives minimal model Sn to de Rham complex  .
.
 .
.
[Interpretation]
Word is given by spherical surface.
Meaning of word is given by elements x1, ....., xn.
Word has minimal model.
Word becomes formal.
Fundamental group of word contains free group of rank b1(M).
Here KARCEVSKIJ's "stable part" is identified to fundamental group and " mobile part" is identified to free group.
--------------------------------------------------------------------------------------------
3.
[Paper on description of language by TANAKA Akio 2011]
[Paper on description of language by TANAKA Akio 2011]
Description of Language
TANAKA Akio
September 9, 2011
TANAKA Akio
September 9, 2011
Manifold M
Cup product map of M 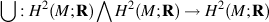
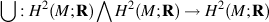
Dual map of 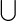

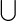

Free Lie algebra that 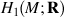 generates £ (
generates £ ( 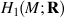 )
)
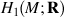 generates £ (
generates £ ( 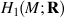 )
)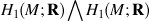 is identified as the partial space of £(
is identified as the partial space of £( 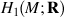 ) that quadrastic Lie bracket of
) that quadrastic Lie bracket of 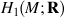 generates.
generates.
Ideal of £( 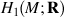 ) that Im η generates a
) that Im η generates a
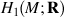 ) that Im η generates a
) that Im η generates a
Holonomy Lie algebra of M 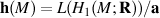
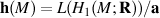
Completion of holonomy Lie algebra 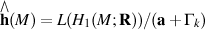
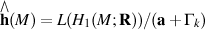
If M has quadrastic homology connection, Malcev completion 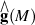 becomes isomorphic with holonoly Lie algebra completion
becomes isomorphic with holonoly Lie algebra completion 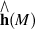 .
.
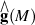 becomes isomorphic with holonoly Lie algebra completion
becomes isomorphic with holonoly Lie algebra completion 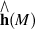 .
.
Primary minimum model M(1)of differential manifold M is isomorphic with Malcev completion of 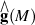 of M's fundamental group.
of M's fundamental group.
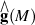 of M's fundamental group.
of M's fundamental group.
For the description of a language model there is a need primary minimum model M(1) of differential manifold M.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
All rights reserved.
© 2011 by The Sekinan Research Field of Language
-----------------------------------------------------------------------------------------------------------
4.
[Note]
If word satisfies Bridgeland 2002's Data{Z, A] , word has a stability in language.
For the problem of additional meaning refer to Karcevskij conjecture 1928 and Kawamata conjecture 2002.
-----------------------------------------------------------------------------------------------------
#This paper is unfinished
Tokyo
25 May 2016
SRFL Theory
25 May 2016
SRFL Theory
Read more: https://srfl-theory.webnode.com/news/derived-category-language-3/
9
Perspective for Derived Category Language. Stability of Language.
TANAKA Akio
1. Model
Derived Category Language.
2. Base
Manifold.
3.Main method
Stability conditions.
4. Theorem
R. Pandharipande and R.P. Thomas. Pandharipande-Thomas Theorem (1998).
K. Behrend. Behrent contructable function (2009).
Y. Toda. Curve-counting theories via stable objects (2010).
T. Bridgeland. Hall algebras and curve-counting invariants (2011).
5. Definition
Mu limit semi-stable object.
6. Space
Mu limit semi-stable object's moduli space.
7. Stability of Language
In the space(6.) language keeps stability as the set of derived duality.
8. Essence of Language
Duality is the essence of language.
Refer to the next.
Derived Category Language, 25 May 2016 Edition.
Actual Language and Imaginary Language. To LÉVI-STRAUSS Claude.
This paper is unfinished.
Tokyo
19 July 2016
Sekinan Library
Read more: https://srfl-paper.webnode.com/news/perspective-for-derived-category-language-stability-of-language/
10
Duality of Language
1. Model
Calabi-Yau 3-folds.
2. Theorem
R. Pandharipande and R.P. Thomas.
Pandharipande-Thomas Theorem (1998).
K. Behrend.
Behrent contructable function (2009).
Y. Toda.
Generating functions of stable pair invariants via wall-crossing in derived categories in algebraic geometry. (2008)
Curve-counting theories via stable objects (2010).
T. Bridgeland.
Hall algebras and curve-counting invariants (2011).
D. Joyce and Y.Song.
A theory of generalized Donaldson-Thomas invariants. (2012)
3. Definition
Generalized DT invariants. ( Joyce and Song. 2012)
4. Isomorphism
Isomorphism is induced in the defined moduli spaces.
5. Duality and mirror
If language is identified as Calabi-Yau 3 folds, language inevitably induce dual or mirror element.
Reference
Rensetsuso no Doraiken ni kakawaru shomondai. TODA Yukinobu. 2016. Sugaku shobo. Tokyo.
Reference 2
Derived Category Language, 25 May 2016 Edition.
Reference 3.
Actual Language and Imaginary Language. To LÉVI-STRAUSS Claude.
Reference 4.
Symplectic Language Theory Note 3 Mirror Symmetry Conjecture on Rational Curve.
Symplectic Language Theory Note 6 Homological Mirror Symmetry Conjecture by KONTSEVICH.
Reference 5.
Main papers of Sekinan Library.
SRFL Paper.
Paper ends.
------------------------------------------------------------------------------------------------------
This paper is unfinished.
Tokyo
22 July 2016
Sekinan Library
Read more: https://srfl-paper.webnode.com/news/duality-of-language-derived-category-language/
Issue Paper 2
Over


No comments:
Post a Comment