Additional meaning and embedding
1.Derived category
Category theoretic mirror symmetry conjecture
1.
Fukaya category is
Fuk(X, ω).
2.
General symplectic manifold is
.
3.
Derived category of A∞
is 
.
4.
Conjecture
When
and 
have physical mirror relation,
there exists the next triangle category's equivalence
2.Embedding
Derived Category Language 2
Kawamata Conjecture
Conjecture
is birational map between smooth objective algebraic manifolds.
And
.
At This condition,
there exists next fully faithful embedding.
3.Stable and mobile
[Preparation]
Graded differential algebra 
Minimal model of graded differential algebra 
Degree of homogenious element x of graded differential algabra |x|
Basis of linear space is given by homogenious and elements x1, ....., xn
Λ (V) = Λ(V)k =Λ (x1, ....., xn )
Operation of minimal model 
<Example>
Spherical surface Sn, n≥2
de Rham complex 
*(Sn)
When n iseaven number,
Volume element of Sn 
Mn = Λ (x), |x| = n, dx = 0,
, 
M2n-1 gives minimal model Sn to de Rham complex 
.
When n is odd number,
Mn gives minimal model Sn to de Rham complex .
[Interpretation]
Word is given by spherical surface.
Meaning of word is given by elements x1, ....., xn.
Word has minimal model.
Word becomes formal.
Fundamental group of word contains free group of rank b1(M).
Here KARCEVSKIJ's "stable part" is identified to fundamental group and " mobile part" is identified to free group.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
4.Additional meaning
For the Supposition of KARCEVSKIJ Sergej
Completion of Language
September 23, 2011
[Preparation]
1.
n dimensional complex space Cn
Open set 
Whole holomorphic function over U 
Ring sheaf for
U →Oan(U)
Complex analytic manifold Cann
Algebraic manifold An multinomial of Cann
Ideal of multinomial ring a 
[x1, x2, ..., xn]
V(a) = {(a1, a2, ..., an) 
Cn f (a1, a2, ..., an) = 0, 
a }
Whole closed set of V(a) 
Fundamental open set D(f) = {(a1, a2, ..., an) Cn | f (a1, a2, ..., an) ≠ 0}
Arbitrary family of open set {Ui} 
Easy sheaf F 
Zariski topological space
Ring sheaf O
Affine space An = ( , O)
Ring R
Set of whole maximum ideal Spm R1
Spm R Spectrum of R
<Proposition>
Spm R is Noether- like.
◊
<Proposition>
R is integral domain.
Whole of open sets without null set Ux
Quotient field K
Mapping from Ux to whole partial set of K O
O(V(a)c) = 
Rf
c expresses complementary set.
O is easy sheaf of ring over Spm R that is whole set K.
◊
<Definition>
R is finite generative integral domain over k.
Triple (i) (ii) (iii) is called affine algebraic variety.
(i) Set Spm R
(ii) Zariski topology
(iii) Ring's sheaf O
O is called structure sheaf of affine algebraic variety.
◊
Ring homomorphism between definite generative integral domains 
Upper is expressed by 
.
Ring holomorphism OX(U) → OY((t
)-1U)
Morphism from affine algebraic variety Y to X ( OX(U) → OY((t )-1U), X→Y )
When 
is surjection, t is isomorphism overclosed partial set defined by p= Ker 
.
Upper is called to closed immersion.
2.
Ring holomorphism
Morphism between affine algebraic varieties 
Kernel of 
p
Image of 
<Definition>
It is called that when is injection 
is dominant.
◊
<Definition>
R is medium ring between S and its quotient field K.
When that is given by natural injection is isomorphism over open set, is called open immersion.
◊
<Definition>
When X is algebraic variety, longitude of maximum chain is equal to transcendental dimension of function field k(X).
It is called dimension of algebraic variety X, expressed by dim X.
◊
<Definition>
Defined generative field over k K
Space ( X, Ox )added ring that is whole sets of K that has open covers {Ui}
satisfies next conditions is called algebraic variety.
(i) Each Ui is affine algebraic variety that has quotient K .
(ii) For each i, j 
I, intersection 
is open partial set of 
.
◊
3.
<Definition>
Tensor product between ring and itself becomes ring by each elements products.
Elements 
that defines surjective homomorphism is expressed by 
.
Image 
of closed embedding defined by is called diagonal.
◊
<Definition>
Field K
Ringed space that have common whole set K (A, OA) (B, OB)
Topological space C
Open embedding 
A and B have common partial set C.
Topological space glued A and B by C 
Easy sheaf over W OW
ahere, arbitrary open set Ø ≠ 
Ringed space 
is called glue of A and B by C.
◊
<Definition>
Intedgral domains that have common quotient field K R, S
Element R am ≠ 0
Element S bn ≠ 0
Spm T 
Spm R, Spm T 
Spm S
Glue defined by the upper is called simple.
◊
<Definition>
Affine algebraic varieties U1, U2
Common open set of U1, U2 UC
Diagonal embedding 
When the upper is closed set, glue is called separated.
◊
<Proposition>
For simple glue 
, next is equivalent.
(*) It is separated.
(**) Ring 
is generated by R and S.
◊
<Definition>
R and S are integral domains that have common quotient field K.
For partial ring T=RS generated by R and S, when <Definition> simple is satisfied, it is called "Spm R ad Spm S are simple glue."
◊
<Sample>
Projective space Pn is simple glue.
◊
<Definition>
Algebraic Variety's morphism is glue of affine algebraic variety's ring homomorphism image.
Algebraic direct product is direct product of affine algebraic variety.
◊
4.
Affine algebraic variety X
Ring over k R
is called R value point of X.
Whole is called set of R value point of X, expressed by X(R).
Ring homomorphism over k 
X(f) := X(R)
X(S)
Ring homomorphism , 
<Definition>
is function from ring category over k to category of set.
◊
<Definition>
Functors from ring category to set category F, G
Ring R
{
}
has functional morphism.
Functors F,G have isomorphism ( or natural transformation).
Functor from ring's category to set's category that is isomorphic to algebraic variety, is called representable or represent by X, or fine moduli.
◊
<Definition>
Functor from ring's category to set's category F
When 
satisfies the next conditions, X is called coarse moduli.
(i) There is natural transformation : 
.
(ii) Natural transformation 
,
Morphism that satisfies 
is existent uniquely.
(iii) For algebraic close field k' 
k, 
(k') is always bijection.
◊
<Definition>
Algebraic variety G that 
is functor to group's category is called algebraic group.
◊
<Definition>
Finite generative ring over k A
When G = Spm A satisfies 3 conditions on the next triad is called affine algebraic group.
Triad
Conditions
(i) 
are commutative for 
.
(ii)There is identity map for A.
(iii) There is coincident with 
for A.
◊
5.
Projective space over C Pn
(2n+1) dimensional spherical surface 
{
}
Pn has continuous surjection from 
.
Pn is compact.
<Definition>
Map 
is called closed map when 
is closed set image 
becomes closed set.
◊
<Definition>
Algebraic variety X is called complete when projection 
is closed map for arbitrary manifold Y.
◊
<Definition>
Morphism from complete algebraic manifold X to separated algebraic manifold Y, 
is closed map.
◊
<Proposition>
Projective space Pn is complete.
◊
<System>
Algebraic manifold that has closed embedding at Pn is complete.
This algebraic manifold is called projective algebraic manifold.
[Interpretation]
Here language is expressed by Pn.
Word is expressed by projective algebraic manifold.
Meaning of word is expressed by closed embedding.
This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language
5.
Note
Provisional philosophic conjecture on additional meaning is the following.
- From symplectic geometry to Fukaya category.
- From Fukaya category to derived category.
- Kawamata conjecture at derived category.
- Smooth objective algebraic manifolds satisfies birational map.
- Fully faithful embedding exists between two manifolds.
[References]
Extract of Zoho papers at Sekinan Library.
More details refer to Sekinan Zoho.
Tokyo
23 May 2016
.
is bounded kernel of t-structure.
gives stability condition on A .
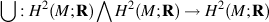
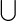
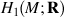generates £ ( 
)
is identified as the partial space of £( 
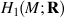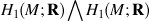
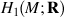) that quadrastic Lie bracket of 
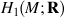generates.
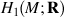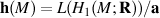
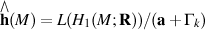
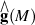) that Im η generates a 
becomes isomorphic with holonoly Lie algebra completion 
.
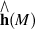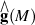of M's fundamental group.
over ring R {
