Root of Language
Root of Language
TANAKA Akio
The root of language is in the discreteness. All the information of language are generated from this simple structure which supposition is derived from Flux Conjecture, Lemma 1 and Lemma 2.
TANAKA Akio
The root of language is in the discreteness. All the information of language are generated from this simple structure which supposition is derived from Flux Conjecture, Lemma 1 and Lemma 2.
Floer Homology Language
TANAKA Akio
Note 8
Discreteness of Language Flux Conjecture(Lalonde-McDuff-Polterovich 1998)Image of Flux homomorphism is discrete at H1(M; R).Lemma
1 Next two are equivalent.
(i) Flux conjecture is correct.
(ii) All the complete symplectic homeomorphism is C1 topological closed at symplectic transformation group.Lemma
2 Next two are equivalent.
(1) Flux conjecture is correct.
(ii) Diagonal set M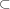 M×M is stable by the next definition.Definition
M×M is stable by the next definition.Definition
L is stable at the next condition.1 Next two are equivalent.
(i) Flux conjecture is correct.
(ii) All the complete symplectic homeomorphism is C1 topological closed at symplectic transformation group.Lemma
2 Next two are equivalent.
(1) Flux conjecture is correct.
(ii) Diagonal set M
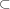 M×M is stable by the next definition.Definition
M×M is stable by the next definition.Definition(i) There exist differential 1 form u1, u2 over L that is sufficiently small.
(ii) When sup|u1|, sup|u2| is Lu1
 Lu2 for u1, u2 ,there exists f that satisfies u1 - u2 = df .Explanation 0
Lu2 for u1, u2 ,there exists f that satisfies u1 - u2 = df .Explanation 0 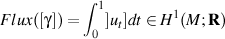
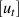 is de Rham cohomology class.Symplectic manifold (M, w)Group's connected component of complete homeomorphism Ham (M, w)Flux isomorphism Flux: π1(Ham(M, w) )→ R Road of Ham (M, w) γ(t)δγ / δt = Xu(t) that is defined bu closed differential form Utover M Explanation
is de Rham cohomology class.Symplectic manifold (M, w)Group's connected component of complete homeomorphism Ham (M, w)Flux isomorphism Flux: π1(Ham(M, w) )→ R Road of Ham (M, w) γ(t)δγ / δt = Xu(t) that is defined bu closed differential form Utover M Explanation1 Symplectic manifold Mn-dimensional submanifold L
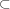 ML that satisfies next condition is called special Lagrangian submanifold.Ω's restriction to L is L's volume.
ML that satisfies next condition is called special Lagrangian submanifold.Ω's restriction to L is L's volume.2 M's special Lagrangian submanifold L Flat complex line bundle LLAGsp(M) (L, L)
3 Complex manifold M†p
 M†Sheaf over M† fpfp (U) = C ( p
M†Sheaf over M† fpfp (U) = C ( p U)fp (U) = 0 ( p
U)fp (U) = 0 ( p 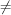 U)
U)4 Special Lagrangian fiber bundle π : M → N Complementary dimension 2's submanifold S(N)
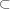 Nπ-1 (p) = LPPair (Lp, Lp)p
Nπ-1 (p) = LPPair (Lp, Lp)p N-S(N)Lp Complex flat line bundle All the pair (Lp, Lp) s is M0† .5(Geometric mirror symmetry conjecture Strominger-Yau-Zaslow 1996)Mirror of M is diffeomorphic with compactification of M0† .6 Pairs of Lagrangian submanifold of M and flat U
N-S(N)Lp Complex flat line bundle All the pair (Lp, Lp) s is M0† .5(Geometric mirror symmetry conjecture Strominger-Yau-Zaslow 1996)Mirror of M is diffeomorphic with compactification of M0† .6 Pairs of Lagrangian submanifold of M and flat U(1) over the submanifold (L1, L1), (L2, L2)(L1, L1)
 (L2, L2) means the next.There exists complete symplectic homeomorphism that is ψ(L2 ) = L2andψ*L2 is isomorphic with L1.Impression Discreteness of language is possible by Flux conjecture 1998.
(L2, L2) means the next.There exists complete symplectic homeomorphism that is ψ(L2 ) = L2andψ*L2 is isomorphic with L1.Impression Discreteness of language is possible by Flux conjecture 1998.[References]
Quantization of Language / Floer Homology Language / Note 7 / June 24, 2009For WITTGENSTEIN Ludwig / Position of Language / Tokyo December 10, 2005 To be continued
Tokyo July 19, 2009
Sekinan Research Field of Language
Back to sekinanlogoshome
................................................................................................................
Source:
Floer Homology Language / Note 8 / Discreteness of Language / 19 July 2009
Tokyo
20 September 2014
Sekinan Research Field Of Language
Floer Homology Language / Note 8 / Discreteness of Language / 19 July 2009
20 September 2014
Sekinan Research Field Of Language
Read more: https://srflnote.webnode.com/news/root-of-language-20-september-2014/

No comments:
Post a Comment