Sekinan Table
Thursday, 30 July 2015
Wednesday, 29 July 2015
Sekinan Study Paper Tokyo 2015
Sekinan Study Paper
Tokyo
2015
Study result of
Sekinan Library
Sekinan Research Field of Language
Zoho
Sekinan Study Paper is the paper site of Sekinan Library and Sekinan Research Field of Language.
Sekinan Library was founded at Tachikawa, Tokyo in 1986 for the study of language.
In 2003, for the specialized study of language universals, Sekinan Research Field of Language was added at Hakuba, Nagano.
Sekinan Library was founded at Tachikawa, Tokyo in 1986 for the study of language.
In 2003, for the specialized study of language universals, Sekinan Research Field of Language was added at Hakuba, Nagano.
Blog for Paper
Blog for News
The summer of Kirigamine Highlands, Nagano, Japan.
I have stayed and written the early time papers at the lodge nearby.
I have stayed and written the early time papers at the lodge nearby.
Friday, 24 July 2015
Infinite Loop Space Language Word as Infinite loop Space
Infinite Loop Space Language
Word as Infinite loop Space
TANAKA Akio
1.
Result of D. G. Quillen by Annals of Mathematics, 96 (1972).
Algebraic K theory over commutative ring R.
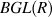is classifying space of 
.
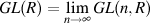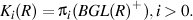
Quillen showed that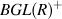 
is infinite loop space.
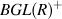is infinite loop space.
2.
Interpretationof Quillen's result.
Meaning of word is expressed by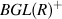 
.
.
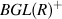Word is expressed by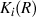 
, 
.
, .
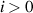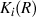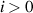Saying in other words.
Word is expressed by high dimensional algebraic K group over commutative ring R.
Conclution at the present.
Word has meaning that is expressed by infinite loop space.
Word has parameter that is expressed by commutative ring.
Word has dimension that belongs to albegraic K group.
Tokyo
6 December 2012
6 December 2012
Sekinan Research Field of Language
Infinite Loop Space language Contents
Infinite Loop Space language |
Word as Infinite Loop Space
Tokyo
24 July 2015 Reprint
Thursday, 23 July 2015
Dual Language Duality of Language
Dual Language
Duality of Language
TANAKA Akio
1. Theorem(Poincaré duality)
For oriented compact n-dimension topological manifold M,
biliear form
is exact,
and 
become dual space each other.
♦
For oriented compact n-dimension topological manifold M,
biliear form
is exact,
and become dual space each other.♦
2. Interpretation
Word := MBoundary of language := pDual language := and Language := 
Word := MBoundary of language := pDual language :=
and Language :=
3. Explanation
Word is compact and has dimension.
Language has dimension.
Language has boundary.
Boundary makes dual language.
Word is compact and has dimension.
Language has dimension.
Language has boundary.
Boundary makes dual language.
4. References
Distance Theory
Mirror Theory
Guarantee of Language
Distance Theory
Mirror Theory
Guarantee of Language
Tokyo
25 May 2012Sekinan Research Field of Language
25 May 2012Sekinan Research Field of Language
Birational Language Elements of Word
Birational Language
Elements of Word
TANAKA Akio
1, Proposition
Weighted projective space
is birationally equivalent with projective space 
.
2. Proposition
Weighted hyperplane
is isomorphic to Weighted projective space .
Weighted hyperplane
is isomorphic to Weighted projective space .
3. Proposition
Weighted projective space is one-to-one correspondent with quotient space 
.
Here G is finite Abellian group to ptrojective space.
.
Weighted projective space
is one-to-one correspondent with quotient space .Here G is finite Abellian group to ptrojective space
. .
4. Definition
The next
is hyperplane defined by equation 
.
.
Here coordinate system
of linear space V is called homogenious coordinate system of projective space 
.
The next
is hyperplane defined by equation . .Here coordinate system
of linear space V is called homogenious coordinate system of projective space .
5. Interpretation
Language:= projective space .
Word:=Weighted hyperplane .
Elements of word:=coordinate system of linear space V .
Language:= projective space
.Word:=Weighted hyperplane
.Elements of word:=coordinate system
of linear space V .
6. Conclution
When elements of word is given at linear space, language is defined at projective space using birational equivalence.
When elements of word is given at linear space, language is defined at projective space using birational equivalence.
Tokyo
April 26, 2012Sekinan Reserach Field of Language
April 26, 2012Sekinan Reserach Field of Language
Birational Language, Dual Language Contents
Birational Language, Dual Language
Tokyo
23 July 2015 Reprint
Genealogical Tree Fourth Edition
Genealogical Tree
..............................................................................................................................
Genealogical Tree
Manuscript of Quantum Theory for Language
|
On Time Property Inherent in Characters
|
Quantum Theory for Language
| |
Distance Theory Property of Quantum
| |
Prague Theory Quantification of Quantum
|
Reversion Theory
|
Mirror Theory
|
Mirror Language
|
Guarantee of Language
|
Actual Language and Imaginary Language
|
Direction
|
Uniformity
|
Changeability
|
Individuality
|
Time
|
Fixation
|
Grammar
|
Substantiality
|
Frame
|
Recognition
|
Ideogram
|
Conversation
|
Descriptiveness
|
Lineation
|
System
|
Automaton
|
Vector
|
Cell Theory
|
From Cell to Manifold <For LEIBNIZ and JAKOBSON>
Conifold as Word
Projective Space as Scheme for Word Order
|
Algebraic Linguistics
|
Sentence versus Word
Deep Fissure between Word and Sentence
|
Distance Theory Algebraically Supplemented
|
Bend
Distance <Direct Succession of Distance Theory>
S3 and Hoph Map
|
Noncommutative Distance Theory
|
Groupoid C*-Algebra
Point Space Atiyah’s Axiomatic System
Kontsevich Invariant
|
Clifford Algebra
|
From Super Space to Quantization
Anti-automorphism
Anti-self-dual Form
Dirac Operator
TOMONAGA's Super Multi-time Theory
Periodicity
Creation Operator and Annihilation Operator
Meaning Product
|
Kac-Moody Lie Algebra
|
Kac-Moody Lie Algebra
Quantum Group
Finiteness in Infinity on Language
|
Operator Algebra
|
Differential Operator and Symbol
<One Paper lost>
Self-adjoint and Symmetry
Frame Operator
Order of Word
Grammar
Recognition
|
von Neumann Algebra
|
von Neumann Algebra 1
Measure
Tensor Product
Compact Operator
von Neumann Algebra 2
Generation Theorem
von Neumann Algebra 3
Properly Infinite
Purely Infinite
von Neumann Algebra 4
Tomita's Fundamental Theorem
Borchers' Theorem
Relation between Word and Sentence
|
Functional Analysis
|
Functional Analysis
Baire's Category Theorem
Equality and Inequality
Space
Functional
Finiteness of Vocabulary
Distance at Hypersurface
Functional Analysis 2
Pre-Hilbert Space and Hilbert Space
Orthogonal Decomposition
Generation of Word
|
Reversion Analysis Theory
|
Reversion Analysis Theory
Reversion Analysis Theory 2
|
Holomorphic Meaning Theory
|
Holomorphic Meaning Theory
Holomorphic Meaning Theory 2
|
Stochastic Meaning Theory
|
Stochastic Meaning Theory
Stochastic Meaning Theory 2
Stochastic Meaning Theory 3
Stochastic Meaning Theory 4
Stochastic Meaning Theory 5
Stochastic Meaning Theory Conjecture 1
Stochastic Meaning Theory Conjecture 2
|
Energy Distance Theory
|
Energy and Distance
Heat and Diffusion
Energy and Functional
Finsler Manifold and Distance
Word and Meaning Minimum
Geometry of Word
|
Complex Manifold Deformation Theory
|
Distance of Word
Reflection of Word
Uniqueness of Word
Amplitude of Meaning Minimum
Time of Word
Orbit of Word
Map between Words
Understandability of Language
|
Language Manifold Theory
|
Moser's Theorem
|
Topological Group Language Theory
|
Word Problem of Word-hyperbolic Group
From Finiteness to Infinity on Language
Boundary of Words
|
Symplectic Language Theory
|
Symplectic Topological Existence Theorem
Gromov-Witten Invariant
Mirror Symmetry Conjecture on Rational Curve
Isomorphism of Map Sequence
Generating Function (Text lost)
Homological Mirror Symmetry Conjecture by KONTSEVICH
Structure of Meaning
On Structure
|
Floer Homology Language
|
Potential of Language
Supersymmetric Harmonic Oscillator
Grothendieck Group
Reversibility of Language
Homology Generation of Language
Homology Structure of Word
Quantization of Language
Discreteness of Language
|
Proto Algebraic Geometry Language
|
Language, Word, Distance, Meaning and Meaning Minimum
|
Imaginary Language
|
Notes for KARCEVSKIJ Sergej, "Du Dualisme asymétrique du signe linguistique"
Condition of Meaning
|
Notes for KARCEVSKIJ Sergej, "Du Dualisme asymétrique du signe linguistique"
Condition of Meaning
|
|
Projective Space Model|
Vector Bundle Model
|
|
|
Hyperbolic Language
|
|
Parts and Whole (AGL Preface)
Dimension of Language (AGL 1)
Synthesis of Meaning and Transition of Dimension (AGL 2)
Birth of Word, Synthesis of Meaning and Dimension of New Word (AGL 3)
Dimension Conjecture at Synthesis of Meaning (AGL 4)
|
Three conjectures for dimension, synthesis and reversion with root and supplement
|
At least three elements for language universals
|
Disposition of Language
Distance of Word
Flow of Language
Papers for Language Dimension, In chronological order
Preparation for the energy of language
Subscribe to:
Posts (Atom)