For MAC LANE Saunders. Categorical Approach toward Language

15/08/2016 22:23

For MAC LANE Saunders

Categorical Approach toward Language　

 

 

Torus Chain

Word Containing Time and 4 Dimensional Sphere

Structure of Word

 

Tokyo April 5, 2007

Sekinan Research Field of Language

www.sekinan.org

Read more: https://srfl-paper.webnode.com/news/for-mac-lane-saunders-categorical-approach-toward-language/

Language between Sergej Karcevskij and string theory, one century's trace / Book and paper index edition :: SRFL Paper

Language between Sergej Karcevskij and string theory, one century's trace / Book and paper index edition :: SRFL Paper

 

The Days of Decipherment

31/07/2016 14:46

The Days of Decipherment

TANAKA Akio

On 20 July 2016 I went Tokyo National Museum, Ueno Park, Tokyo to see the exhibition AJOURNEY TO THE IMMORTALS: TREASURES OF ANCIENT GREECE, where I saw the linear A and B. It reminds me the youth days, so to say, the days of decipherment.

1960s -1970s is the age of decipherment in a sense. I was age 20 in 1967 and was learning language and literature at university. In 1958 John Chadwick's THE DECIPHERMENT OF LINEAR B was published from Cambridge University Press. At the preface of the book he wrote that the decipherment of linear B was told  at Documents in Mycenaean Greek (Cambridge University Press, 1956) and Michael Ventris that deciphered the Linear B.

In the same age in Japan, Xixia wenzi (Xixia characters) in China was deciphered byNISHIDA Tatsuo (1928-2012) who wrote the analysis and grammar of Xixia characters through the paper Seikamoji no bunseki narabini Seikago bunpou no kenkyuu in 1962.
In almost the same time, Inca characters were studying to decipher. I frequently heard that Russian team developed largely.

In early 1970s I frequently went to Kanda, Tokyo where old bookshops were selling vast Oriental books at the Hakusan street and Yasukuni Street. I bought Chinese classics, especially linguistic classics written in the Qing dynasty and I read them almost every day containing the comparison with the western linguistic results. The Qing dynasty's heritage were DUAN Yucai, WANG Niansun, WANG Yingzhi and WANG Guowei and so forth. DUAN Yucai's Showenjezi zhu and WANG Guowei's Guantang jilin  were the most important for me.

In France, 1960s was the days of Bourbaki that was one of the decipher of geometry by algebra, at least I thought so at that time. I sought and bought several Bourbaki's books at the old bookshops in Kanda, Tokyo,which is the largest old bookshop streets in Japan. But from my ability to mathematics Bourbaki was too much difficult to read on. From the days the long and winding road began to mathematics and its applicable study for language universals.

At the exhibition of ancient Greece I confirmed in particular that the stability of language was  kept by letters and characters from the Linear A and Linear B. 

Exhibition Catalogue numbers are the next.
The numbers 39 and 40 are Linear A. 41 and 77 are Linear B.

39. Clay juglet c. 1800 B.C. ~ c. 1700 B.C.
40. Clay bar c. 1700 B.C. ~ c. 1650 B.C.
41. Clay tablet c. 1375 B.C. ~ c. 1350 B.C.
77. Linear B bar and tablet c. the 13th century B.C.

For my part the stability  has been one of the biggest themes on language phenomena since I was taught from CHINO Eiichi through the results of the Linguistic Circle of Prague, especially of Sergej Karcevskij.


 

The exhibition catalogue and Chadwick's book Japanese translated edition.

 

 

Reference

1. Essence of Language / SRFL Paper 
2. Derived Category Language, 26 July 2016 Edition

References 2

1. The Time of WANG Guowei
2. 40 years passed from I read WANG Guowei

References 3

1. Meaning Minimum On Roman Jakobson, Sergej Karcevskij and CHINO Eiichi
2. Half Farewell to the Linguistic Circle of Prague and Sergej Karcevskij
3. Sergej Karcevskij, Soul of Language
4. Gift from Sergej Karcevskij
5. Follower of Sergej Karcevskij
6. For KARCEVSKIJ Sergej
7. Notes for KARCEVSKIJ Sergej / Note for KARCEVSKIJ Sergej's "Du dualisme asymetrique du signe linguistique"

References 4

1. Fortuitous Meeting
2. ​Linguistic Circle of Prague
3. Prague in 1920s
4. Under the dim light

References 5

1. The Time of Language, Ode to The Early Bourbaki To Grothendieck
2. Bourbaki' ELEMENTS DE MATHEMATIUE Troisieme edition, 1964

Tokyo

30 July 2016

Sekinan Library

Read more: https://srfl-paper.webnode.com/news/the-days-of-decipherment/

 

Essence of Language

26/07/2016 22:28

Essence of Language
Seeing the exhibition TREASURES OF ANCIENT GREECE, Tokyo National Museum

TANAKA Akio

20 July 2016 I went to see the exhibition A JOURNEY TO THE IMMORTALS: TREASURES OF ANCIENT GREECE being opened at Tokyo National Museum, Ueno,Tokyo.

At the exhibition I first saw  Linear A and Linear B.
Exhibition Catalogue numbers are the next.
The numbers 39 and 40 are Linear A. 41 and 77 are Linear B. 

39. Clay juglet
40. Clay bar
41. Clay tablet
77. Linear B bar and tablet

 About the two Linear I knew the brief information from the book, THE DECIPHERMENT OF LINEAR B by John Chadwick, Cambridge University Press, 1960.
From the exhibition I also knew still now not to decipher the Linear A.
My simple impression  is the next.
If the stability of language exist in the structure, the essence of language is appeared at the letters and characters. So I think. The core of this view contains the view for structure of language, which I would be able to write clearly using mathematics. For more details, refer to the reference 2.

References
A JOURNEY TO THE IMMORTALS: TREASURES OF ANCIENT GREECE  [Exhibition Catalogue]. Tokyo National Museum et al. 2016.
THE DECIPHERMENT OF LINEAR B by John Chadwick, Cambridge University Press, 1960.

Reference 2
Perspective for Derived Category Language.Stability of Language

Reference 3
Derived Category Language, 23 July 2016 Edition


Tokyo
27 July 2016
SekinanLibrary

Tokyo National Museum, Ueno,Tokyo

Read more: https://srfl-paper.webnode.com/news/the-essence-of-language/

 

Duality of Language. Derived Category Language

22/07/2016 18:41

Duality of Language

 

TANAKA Akio

1. Model
Calabi-Yau 3-folds.

2. Theorem
R. Pandharipande and R.P. Thomas.  
Pandharipande-Thomas Theorem (1998).
K. Behrend. 
Behrent contructable function (2009).

Y. Toda. 
Generating functions of stable pair invariants via wall-crossing in derived categories in algebraic geometry. (2008)
Curve-counting theories via stable objects (2010).
T. Bridgeland. 
Hall algebras and curve-counting invariants (2011).
D. Joyce and Y.Song. 
A theory of generalized Donaldson-Thomas invariants. (2012)

3. Definition
Generalized DT invariants. ( Joyce and Song. 2012)

4. Isomorphism
Isomorphism is induced in the defined moduli spaces.

5. Duality and mirror
If language is identified as Calabi-Yau 3 folds, language inevitably induce dual or mirror element.

Reference
Rensetsuso no Doraiken ni kakawaru shomondai. TODA Yukinobu. 2016. Sugaku shobo. Tokyo.

Reference 2
Derived Category Language, 25 May 2016 Edition.

Reference 3.
Actual Language and Imaginary Language. To LÉVI-STRAUSS Claude.

Reference 4.
Symplectic Language Theory ​ Note 3 Mirror Symmetry Conjecture on Rational Curve​.
Symplectic Language Theory ​ Note 6 Homological Mirror Symmetry Conjecture by KONTSEVICH​.

Reference 5.
Main papers of Sekinan Library.
SRFL Paper.

Paper ends. 
-----------------------------------------------------------------------------------------------------------------------

This paper is unfinished.

Tokyo
22 July 2016
Sekinan Library

Read more: https://srfl-paper.webnode.com/news/duality-of-language-derived-category-language/

Perspective for Derived Category Language. Stability of Language :: SRFL Paper

Perspective for Derived Category Language. Stability of Language :: SRFL Paper

Derived Category Language 3

 

Derived Category Language 3

Language stability and triangulated category

 

[Epitome]

T. Bridgeland defined stability conditions on triangulated categories in 2007.
Language's stability presented by Sergej Karcevskij in 1928.
Bridgeland's stability seems to hint for  Karcevskij's stability.

 

Stability conditions on triangulated categoriesData ( Z, A ) satisfies the next condition.

  is bounded kernel of t-structure. gives stability condition on A .

 

------------------------------------------------------------------------------------------------------

2.
[Paper on Karcevskij conjecture by TANAKA Akio 2011]

 

Notes for KARCEVSKIJ Sergej

Condition of Meaning
TANAKA Akio
September 11, 2011

[Preparation]

Graded differential algebra 

Minimal model of graded differential algebra 

Degree of homogenious element x of graded differential algabra |x|

Basis of linear space is given by homogenious and elements x₁, ....., x_n

N  (V) =  L (V) _k  = N  ( x ₁ , .....,  x _n  )

Operation of minimal model 

Spherical surface Sⁿ, n≥2

de Rham complex *(Sⁿ)

When n iseaven number,

Volume element of S_n 

M_n = Λ (x), |x| = n, dx = 0,

, 

M_2n-1 gives minimal model S_n to de Rham complex  .

When n is odd number,

M_n gives minimal model S_n to de Rham complex  .

[Interpretation]

Word is given by spherical surface.

Meaning of word is given by elements x₁, ....., x_n.

Word has minimal model.

Word becomes formal.

Fundamental group of word contains free group of rank b₁(M).

Here KARCEVSKIJ's "stable part" is identified to fundamental group and " mobile part" is identified to free group.

Refer to the paper  Notes for KARVESKIJ Sergej "asymmetric Dusualisme the linguistic sign"  .

 

--------------------------------------------------------------------------------------------

 

3.
[Paper on description of language by TANAKA Akio 2011]

 

Notes for KARCEVSKIJ Sergej

Description of Language
TANAKA Akio
September 9, 2011

Manifold M

Cup product map of M 

Dual map of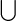  

Free Lie algebra that 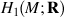 generates £ (  )

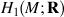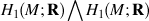 is identified as the partial space of £(  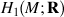) that quadrastic Lie bracket of  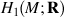generates.

Ideal of £( 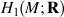 ) that Im η generates a 

Holonomy Lie algebra of M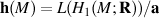 

Completion of holonomy Lie algebra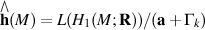 

If M has quadrastic homology connection, Malcev completion 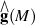 becomes isomorphic with holonoly Lie algebra completion  .

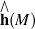Primary minimum model M(1)of differential manifold M is isomorphic with Malcev completion of 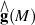 of M's fundamental group.

For the description of a language model there is a need primary minimum model M(1) of differential manifold M.

 

 

 

 

 

This paper has been published by Sekinan Research Field of Language.
All rights reserved.
© 2011 by The Sekinan Research Field of Language

 

-----------------------------------------------------------------------------------------------------------

 

4.

[Note]

If word satisfies Bridgeland 2002's Data{Z, A] , word has a stability in language.

For the problem of additional meaning refer to Karcevskij conjecture 1928 and Kawamata conjecture 2002.

 

-----------------------------------------------------------------------------------------------------

 

#This paper is unfinished

 

Tokyo
25 May 2016
SRFL Theory

Read more: https://srfl-theory.webnode.com/news/derived-category-language-3/

Derived Category Language

 

Derived Category Language

 Derived Category Language

 

1. Bridge between mathematics and physics / Revised

2. Kontsevich's conjecture Category theoretic mirror symmetry conjecture

3. Derived Category Language 1

4. Karcevskij conjecture 1928 and Kawamata conjecture 2002

5. Additional meaning and embedding

6. Derived Category Language 2

7. Language stability and triangulated category

8. Derived Category Language 3

9. Stability of Language

10. Duality of Language

11. Essence of Language

12. The Days of Decipherment

13. Language between Sergej Karcevskij and string theory, one century's trace

 

Reference

1. For MAC LANE Saunders. Categorical Approach toward Language

Read more: https://srfl-paper.webnode.com/news/derived-category-language1/

Perspective for Derived Category Language. Stability of Language :: SRFL Paper

Perspective for Derived Category Language. Stability of Language :: SRFL Paper

Language stability and triangulated category :: SRFL Theory

Language stability and triangulated category :: SRFL Theory

 

Derived Category Language 2 Kawamata Conjecture

19/05/2016 23:08

Derived Category Language 2

Kawamata Conjecture

 

Conjecture

 

is birational map between smooth objective algebraic manifolds.

And

.

At This condition,

there exists next fully faithful embedding.

.

 

[Reference]

1. TODA Yukinobu. Several problems on derived category of coherent sheaf.  Tokyo, 2016.Chapter 6, derived category of coherent sheaf and birational geometry page 148 Conjecture 6.43.

[References 2]

1. Bridge across mathematics and physics
2. Kontsevich's conjecture Category theoretic mirror symmetry conjecture

[Reference 3]

1. Stability of Language / Language and Spacetime

 

Tokyo

19 May 2016

SRFL Theory

Read more: https://srfl-theory.webnode.com/news/derived-category-language-2-kawamata-conjecture/